Estamos acostumbrados a sumar y restar números naturales, o lo que es lo mismo, sólo con números positivos. Pero con los números enteros, tendremos que operar números negativos y eso al principio nos desconcierta un poco.
La diferencia de sumar y restar números enteros de cuando sumamos y restamos con números naturales es que ahora tenemos números negativos.
La Suma de Números Enteros
En la suma de números enteros se presentan los siguientes casos:
• Suma de enteros positivos.
• Suma de enteros positivos con enteros negativos.
• Suma de enteros negativos.
Caso 1: Suma de enteros positivos
Si un número no tiene signo normalmente significa que es un número positivo.
Ejemplo:
5=+5 1=+1
Ley de los Signos para Suma
Para sumar enteros positivos, se suman sus valores y se le coloca el signo + al resultado.
Ejemplos:
(+1)+(+2)=+3
(+5)+(3)=+8
Caso 2: Suma de Enteros Positivos con Negativos
Para sumar enteros positivos con negativos, se restan sus valores y al resultado se le escribe el signo del que tenga mayor valor.
Ejemplos:
(+5) + (-7) = (-2)
(-3) + (+8) = (+5)
Caso 3: Suma de Enteros Negativos
Para sumar enteros negativos, se suman sus valores y al resultado se le escribe el signo menos (-).
Ejemplos:
(– 3) + ( – 8) = – 11
(– 3) + (– 10) = –13
Ley de los signos para la resta
En este caso la ley aplica en el mismo sentido de la suma, poniéndose en práctica las mismas reglas.
(+6) – (+2)= +4
(-7) – (-4)= -3
Ley de los signos para multiplicación y división
Para estas operaciones se aplican las mismas reglas que en la suma:
- En el caso de multiplicar o dividir un signo positivo con otros positivo el resultado es positivo.
- De multiplicar o dividir un signo negativo con otro negativo el resultado será positivo.
- Por último, si se multiplica o divide un signo negativo con uno positivo o viceversa siempre será negativos, sin tomar en cuenta el mayor valor del número.
Ejemplo:
Ubicación de puntos en el eje cartesiano
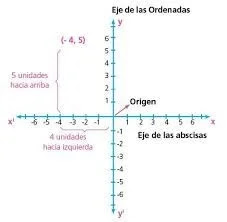
El plano cartesiano está formado por dos rectas numéricas perpendiculares, una horizontal y otra vertical que se cortan en un punto. La recta horizontal es llamada eje de las abscisas o de las equis (x), y la vertical, eje de las ordenadas o de las yes, (y); el punto donde se cortan recibe el nombre de origen(a veces sencillamente ), 0 y tiene por coordenadas (0,0).
Para localizar un punto (x,y) en el plano cartesiano se toma como referencia el origen, a partir de él, se avanza tanto como lo indique el primer número (la abscisa o ejes de la x) hacia a la derecha si es positivo o hacia la izquierda si es negativo, y a parte de esta nueva posición se avanza tanto como lo indique el segundo número (la ordenada o ejes de la y).
Por ejemplo: ubique en el plano cartesiano los siguientes puntos.
P=(x , y)
A= (-5, 3)
B= (6, 5)
C= (4,5 y 3,5)
D= (0,0)
MATERIAL DE APOYO
1.-Explica brevemente la ley de la suma y sus casos. La de la resta y la de la multiplicación y división.
a)¿Qué es un eje cartesiano?;b) Utilidad; c)¿Cómo se llama el eje de la X y el de las Y?;d)¿Dónde se ubican los números positivos y negativos en cada eje?.
2.-Resuelve los ejercicios planteados aplicando la Ley de signos para sumar y restar.
1.-Resuelve las siguientes operaciones con números positivos y negativos.
2.-Resuelve las multiplicaciones de números enteros.
3.-Resuelve las divisiones de números enteros.
4.-Representa los puntos de las Coordenadas siguientes:
Nota: esta semana tendremos dos clases de matemática por favor estar atento a las publicaciones.